FUNCIONES EXPONENCIALES
GRAFICA DE GEOGEBRA
¿QUE SON?
| Funciones exponenciales | |
|---|---|
 Gráfica de Funciones exponenciales | |
| Definición | 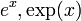 |
| Tipo | Función real |
| Dominio |  |
| Codominio | 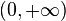 |
| Imagen | 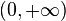 |
| Propiedades | Biyectiva Convexa Estrictamente creciente Trascendente |
| Cálculo infinitesimal | |
| Derivada |  |
| Función primitiva |  |
| Función inversa |  |
| Límites |   |
| Funciones relacionadas | Logaritmo |
La función exponencial, es conocida formalmente como la función real ex, donde e es el número de Euler, aproximadamente 2.71828...; esta función tiene por dominio de definición el conjunto de los números reales, y tiene la particularidad de que su derivada es la misma función. Se denota equivalentemente como f(x)=ex o exp(x), donde e es la base de los logaritmos naturales y corresponde a la función inversa del logaritmo natural.
En términos mucho más generales, una función real E(x) se dice que es del tipo exponencial en basea si tiene la forma
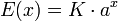
siendo a, K ∈ R números reales, con a > 0. Así pues, se obtiene un abanico de exponenciales, todas ellas similares, que dependen de la base a que utilicen.
La función exponencial ex puede ser definida de diversas maneras equivalentes entre sí, como una serie infinita. En particular puede ser definida como una serie de potencias:

o como el límite de la sucesión:

Propiedades: La función exponencial (y exponenciales en base distinta a e) satisfacen las siguientes propiedades generales.
- Son las únicas funciones que son igual a su derivada (multiplicada por una constante, en el caso de que tengan una base distinta a e)



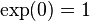
DerivadaLa importancia de las funciones exponenciales en matemática y ciencias radica principalmente de las propiedades de su derivada. En particular,
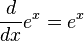
Es decir, ex es su propia derivada . Es la única función con esa propiedad (sin tomar en cuenta la multiplicación de la función exponencial por una constante). Otras formas de expresar lo anterior:
- La pendiente del gráfico en cualquier punto es la altura de la función en ese punto.
- La razón de aumento de la función en x es igual al valor de la función en x.
- La función es solución de la ecuación diferencial
 .
.
Si la base de la función exponencial es cualquier número real a mayor que 0, entonces su derivada se puede generalizar así:

donde la función ln(a) es el logaritmo natural de a. En el caso particular de a = e resulta que ln(e) = 1 y por lo tanto  .
.



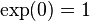
 .
.|
7 Agosto 2013, Creado con GeoGebra |
|
7 Agosto 2013, Creado con GeoGebra |

No hay comentarios:
Publicar un comentario