FUNCION INYECTIVA

FUNCIÓN INYECTIVA

Una función f es inyectiva si, cuando f(x) = f(y), x = y.

Ejemplo: f(x) = x² del conjunto de los números naturales  a  es una función inyectiva.

(Pero f(x) = x² no es inyectiva cuando es desde el conjunto de enteros 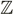 (esto incluye números negativos) porque tienes por ejemplo

• f(2) = 4  y f(-2) = 4)

Nota: inyectiva también se llama "uno a uno", pero esto se confunde porque suena un poco como si fuera biyectiva.

Otras formas de definirse:

Una función  f: " Xà Y", es inyectiva si a cada valor del conjunto "X" (dominio) le corresponde un valor distinto en el conjunto "Y "(imagen) de "f", es decir a cada elemento del conjunto "Y" le corresponde un solo valor de "X"  tal que, en el conjunto "X" no puede haber dos o mas elementos que tengan la misma imagen.

O dicho de otra manera:

Una función es inyectiva si cada f(x) en el recorrido es la imagen de exactamente un único elemento del dominio. En otras palabras, de todos los pares (x,y) pertenecientes a la función, las y no se repiten.Para determinar si una función es inyectiva, gratificamos la función por medio de una tabla de pares ordenados. Luego trazamos líneas horizontales para determinar si las y (las ordenadas) se repiten o no.

EJEMPLO 1 : Determinar si la siguiente función es o no inyectiva: f(x) = x² – 2

Asignando valores a "x" y representándolos en la tabla resulta:

x	-3	-2	-1	0	1	2	3
f(x)	5	2	-1	-2	-1	2	5

:Donde su gráfica será

EJEMPLO 2: Determinar si la siguiente función es o no inyectiva: g(x) = 1 – x³.

Asignando valores a "x" y representándolos en la tabla resulta:

x	-3	-2	-1	0	1	2	3
f(x)	28	9	2	1	0	-7	-26

Donde su gráfica seráa:

 Si hay duda sobre su entendimiento veamos otra forma de expresión matemática y sus ejemplos:

Una función es inyectiva si a cada elemento del rango o imagen se le asocia con uno y solo un elemento del domino.

Ejemplo 1:

Sea A={1,2,3} B={1,2,3}; 

  f: A.B: 

f={(1,2), (2,1), (3,3)}

Es decir, gráficamente queda:

Este es un Applet de Java creado con GeoGebra desde www.geogebra.org – Java no parece estar instalado Java en el equipo. Se aconseja dirigirse a www.java.com 7 Agosto 2013, Creado con GeoGebra

Este es un Applet de Java creado con GeoGebra desde www.geogebra.org – Java no parece estar instalado Java en el equipo. Se aconseja dirigirse a www.java.com 7 Agosto 2013, Creado con GeoGebra